Hello Nature

Essay to say hello nature

3.11大震災への追悼, My 13th Memorial for the 3.11 Great Earthquake – Part 2

放射性崩壊, Radioactive decay

ラザフォードとソディの法則, Rutherford and Soddy law

宇宙ができる過程で多くのエネルギーを得て生じた原子核には、陽子と中性子の数のバランスが悪く不安定な核種も存在します。そのような核種は、放射線を出してエネルギーを減らし安定な核子構成の原子に変化する放射性崩壊を起こす[4]ことが明らかにされました。

ラザフォードとソディは、単位時間に放射性崩壊する原子核数の割合は一定であること、放射能は時間と共に指数関数に従って減衰することを発見しました。この明快な式はラザフォードとソディの法則[5]として知られています。

N(t)を時刻 t における残存原子数、λ を核種に固有の崩壊定数とすれば次式になります。

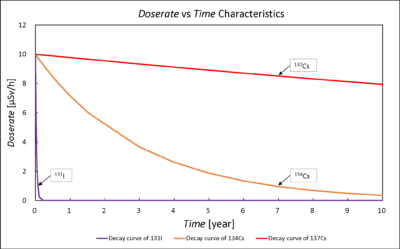
Fig. 2 放射性同位体（ヨウ素131、セシウム134、セシウム137）の放射能は時間と共に指数関数に従って減衰する。
Radioactivity of radioisotopes (Iodine-131, Cesium-134, Cesium-137) decays exponentially with time.
     N(t) = N0 e-λt               (1)

ここでN0は時刻t=0における原子核数です。

放射性原子の半分が他の原子に変化するのにかかった時間を半減期（英: half life）[4]と呼びます。半減期は核種によって変動の少ない物理量として観測されることが分かっています。このことから、半減期を測定すれば、その核種を特定できます。

測定される放射線量率Doserateは放射能に比例するので、aを定数とすれば式1から次式を得ます。

     Doserate = αλN(t) = αλN0 e-λt                     (2)

両辺の自然対数をとれば

     ln(Doserate) = ln(αλN0) - λt                        (3)
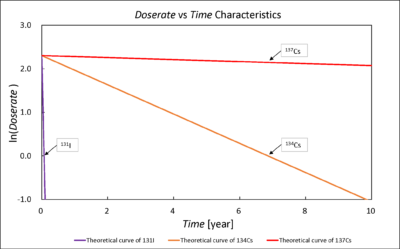
Fig. 3 放射能の対数と時間の関係は直線になり、傾きの絶対値は崩壊定数となる。
Semi-logarithmic plot of radioactivity and time shows a straight line and absolute value of the slope gives the decay constant.

となるので、ln(Doserate)と t のグラフは傾き －λ の直線となります。

Rutherford and Soddy law

Among the atomic nuclei that gained a lot of energy during the creation of the universe, there are some nuclides that are unstable due to an imbalance in the number of protons and neutrons. It has been shown that such nuclides undergo radioactive decay, in which they emit radiation, reduce their energy, and change into atoms with a stable nucleon configuration.[4] Rutherford and Soddy discovered that the rate of radioactive decay of atomic nuclei per unit time is constant and that radioactivity decays exponentially with time. This straightforward formula is known as Rutherford and Soddy’s law.[5]

Suppose N(t) is the number of atoms remaining at time t and λ is the decay constant specific to the nuclide, the following equation is obtained.

     N(t) = N0 e-λt                                       (1)

where N0 is the number of atomic nuclei at t=0.

The time it takes for half of a radioactive atom to change into another atom is called the half-life.[4] It is known that half-life is observed as a physical quantity with little variation depending on the nuclide. From this, the nuclide can be identified by measuring its half-life.

The measured radiation dose rate, Doserate, is proportional to radioactivity, so if a is a constant, the following equation can be obtained from Equation (1).

     Doserate = αλN(t) = αλN0 e-λt                     (2)

 If we take the natural logarithm of both sides,

     ln(Doserate) = ln(αλN0) - λt                        (3)

Therefore, the graph of ln(Doserate) and t is a straight line with slope –λ.

References

4. 放射性崩壊, Wikipedia, https://ja.wikipedia.org/wiki/%E6%94%BE%E5%B0%84%E6%80%A7%E5%B4%A9%E5%A3%8A

5. E. Rutherford and F. Soddy, Philosophical Magazine 4, 370-96 (1902), https://web.lemoyne.edu/~giunta/ruthsod.html

to be continued…

Post-Time:
TOP